ІІІ етап Всеукраїнської олімпіади з інформатики
(Житомирська область)

 31 січня 2025 р.

Задача A. Програмний код

Відомо, що Сергій кожного робочого дня пише A рядків програмного коду. Щотижня він працює B днів, а решту часу відпочиває. Сергій вирішив працювати протягом C тижнів поспіль. Необхідно визначити, скільки рядків коду Сергій напише за цей період.

Вхідні дані. Три рядки, в кожному з яким по одному цілому числу:

· A — кількість рядків коду, які Сергій пише за один робочий день (0 ≤ A ≤ 10000).

· B — кількість робочих днів у тижні (0 ≤ B ≤ 7).

· C — кількість тижнів, протягом яких Сергій буде працювати (0 ≤ C ≤ 500).

Вихідні дані. Вивести одне число — кількість рядків коду, які Сергій напише за C тижнів.

Приклад вхідних даних	Приклад вихідних даних	Пояснення
5 3 4	60	Пояснення: Сергій працює 3 дні на тиждень і пише по 5 рядків кожного дня. За один тиждень він напише 3 * 5 = 15 рядків коду. За 4 тижні він напише 4 * 15 = 60 рядків коду.

Задача B. Мінімальна сума різниць

Дано масив цілих чисел A довжини N. Знайдіть таку перестановку елементів масиву, щоб сума модулів різниць між сусідніми елементами була мінімальною. Іншими словами, потрібно знайти такий порядок елементів масиву, щоб значення
|A₁ – A₂| + |A₂ – A₃| + ... + |A_N–1 – A_N| було мінімальним.

Вхідні дані. В першому рядку записане ціле число N (2 ≤ N ≤ 10⁵) – кількість елементів у масиві.

У другому рядку через один пробіл записано N цілих чисел А₁, А₂, …, A_N (-10⁵ ≤ A_i ≤ 10⁵,
1 ≤ i ≤ N).

Вихідні дані. Виведіть одне число – найменшу суму модулів різниць між сусідніми елементами для оптимальної перестановки масиву.

Приклад вхідних даних	Приклад вихідних даних	Пояснення
3 4 2 1	3	Оптимальна перестановка масиву: [4, 2, 1] або [1, 2, 4]. Сума різниць: |4 – 2| + |2 – 1| = 3

Задача C. Аналіз рядків

Дано N рядків. Для кожного рядка необхідно визначити його тип:

· чисто текстовий рядок – містить лише літери латинського алфавіту (як маленькі, так і великі);

· числовий рядок – містить лише цифри;

· змішаний рядок – містить одночасно латинські літери, цифри та інші символи.

Ваша задача — підрахувати кількість рядків кожного типу.

Вхідні дані. В першому рядку записане ціле число N (1 ≤ N ≤ 10⁴) – кількість рядків у вхідних даних. Наступні N рядків містять самі рядки. Довжина кожного рядка не перевищує 10⁴ символів.

Вихідні дані. Виведіть три числа, розділених пробілом:

· кількість чисто текстових рядків;

· кількість числових рядків;

· кількість змішаних рядків.

Приклад вхідних даних	Приклад вихідних даних
5 example 987654321 abc123 456xyz !!	1 1 3

Задача D. Іспит в університеті

Професор одного з університетів Житомира приймає екзамен у групи з K студентів, які мають однаковий рівень знань.

Професор дуже поспішає і хоче за мінімальний час оцінити знання своїх студентів. Тому професор підготував N задач, рівень складності яких він оцінив від 1 до N балів. Всі задачі мають різний рівень складності. Рівень знань студента оцінюється в R балів, якщо він може розв’язати задачу, яка має рівень складності R, при цьому він не може розв’язати задачу, яка має рівень складності R + 1.

Вважається, що якщо студент не розв’язав якусь задачу, то він не зможе розв’язати ніяку іншу більш високого рівня складності. А якщо студент розв’язав якусь задачу, то він зможе розв’язати будь-яку більш простішу задачу. Якщо він не може розв’язати задачу 1 рівня складності, то його знання оцінюються в 0 балів. Якщо ж студент розв’язав задачу рівня складності N, то він отримує N балів.

При цьому сам екзамен проходить наступним чином: професор вибирає задачу і дає її студенту. Якщо студент розв’язує її за 1 хвилину, то професор дає йому ще одну задачу. Якщо ні – то студент виходить з аудиторії.

Напишіть програму, яка дає відповідь на питання: за який мінімальний час (в хвилинах) професор може гарантовано визначити рівень знань своїх студентів?

Вхідні дані. В першому рядку через пробіл записані числа K та N (1 ≤ K ≤ 100, 1 ≤ N ≤ 1000).

Вихідні дані. Єдине число – результат.

Приклад вхідних даних	Приклад вихідних даних	Пояснення
2 3	2	В даному випадку студенту пропонується задача рівня складності 2. Якщо він не розв’язує її – то наступному студенту пропонується задача рівня складності 1, інакше першому студенту пропонується задача 3 рівня складності

Задача E. Шлях математика

По дорозі на роботу після сильної зливи математик дійшов до автомобільної дороги, яка була майже повністю залита водою. Математик зупинився на самому краю, думаючи як йому перейти на той бік дороги.

Коли він розмірковував, побачив цікавий факт: над водою було видно окремі круглі островки – кришки люків.

Математик ввів систему координат, початок якої був його місцем знаходження, вісь х він направив вздовж краю дороги. Потім він записав координати кожного люка та їх радіуси.

Напишіть програму, яка визначить чи можна перейти через дорогу, не намочивши ноги математику, якщо відома ширина дороги (при цьому треба врахувати, що сторони дороги паралельні) і максимально можливий розмір кроку математика.

Вхідні дані. В першому рядку через пробіл записані три числа:

· W – ширина дороги (дійсне число);

· S – максимальна величина кроку математика (дійсне число);

· N – кількість люків (ціле число, 1 ≤ N ≤ 1000).

В кожному з N наступних рядків записано по три дійсні числа X_i, Y_i, R_i – координати та радіус кожного з люків (дійсні числа).

Вихідні дані. Єдине число – мінімальна кількість люків, через які математик може перейти дорогу, або число «-1», якщо це не можливо зробити.

Приклад вхідних даних	Приклад вихідних даних
15 5 3 -3 6 2.3 0 10 1.5 7 8 0.5	2

Задача F. Підрахунок кількості фігур

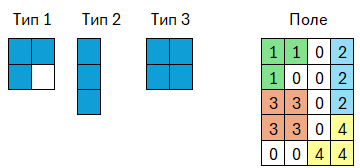
На прямокутному полі розміщено M фігур, які не перетинаються, але можуть дотикатися. Кожна фігура належить до одного з N типів. Типи фігур задано матрицями, які складаються з чисел 1 (заповнена клітинка) та 0 (порожня клітинка). Фігури при розміщенні на полі можуть бути повернуті на 90°, 180° або 270°, а також віддзеркалені по горизонталі та вертикалі. Відомо, що фігури є зв’язними (за вертикальною та горизонтальною суміжністю).

Поле задано матрицею розміру H x W та містить числа від 1 до M, які вказують на частини відповідних фігур. Клітинки з однаковими числами утворюють одну фігуру. Усі клітинки, що належать одній фігурі, утворюють суцільну зв’язану область (за вертикальною та горизонтальною суміжністю).

Вхідні дані. В першому рядку записане ціле число N (1 ≤ N ≤ 100) – кількість типів фігур. Далі йде опис N фігур. Опис кожної фігури розпочинається рядком з двома числами – шириною та висотою i-ої фігури K_i x L_i. Далі розміщується K_i рядків, у кожному з яких L_i чисел 0 або 1, що визначають форму фігури. Далі розміщено рядок з розмірами поля H, W (1 ≤ H, W ≤ 100). Наступні рядки містять матрицю H × W, яка складається з чисел від 0 (порожня клітинка) до M (номер фігури), де кожне число вказує на відповідну фігуру.

Вихідні дані.

Якщо серед типів фігур є еквівалентні (тобто такі, що отримуються одна з одної шляхом поворотів або віддзеркалень), то виведіть  -1. Якщо на полі зустрічається хоча б одна невідома фігура (не відповідає жодному із типів фігур), теж виведіть -1.

Інакше виведіть N чисел – кількість використаних фігур кожного типу в порядку їхнього опису у вхідних даних.

Приклад вхідних даних	Приклад вихідних даних	Пояснення
3 2 2 1 1 1 0 3 1 1 1 1 2 2 1 1 1 1 5 4 1 1 0 2 1 0 0 2 3 3 0 2 3 3 0 4 0 0 4 4	2 1 1	Тип 1 – використано 2 рази (фігури №1 і №4). Тип 2 – використано 1 раз (фігура №2). Тип 3 – використано 1 раз (фігура №3).

Задача G. Атомний реактор

Пластини урану завантажуються в атомний реактор стопками по N пластин. Щоб ефективно контролювати процес реакції,  між пластинами вставляють датчики. Не допускається, щоб більш ніж К пластин, які йдуть підряд в стопці йшли без датчиків між ними. Потрібно визначити, скільки різних стопок пластин можна скласти, дотримуючись цих умов, якщо в кожній стопці повинно бути рівно M датчиків. Всі датчики при цьому мають бути розміщені тільки між пластинами по одному. 

Вхідні дані. В одному  рядку через пробіл записані три числа N, M та K
(0 < N ≤ 100, 1 ≤ M < N, 1 ≤ K ≤ N).

Вихідні дані. Єдине число – результат.

Приклад вхідних даних	Приклад вихідних даних
5 2 2	3